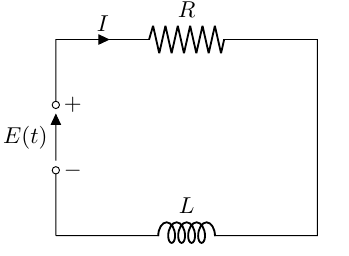
本項では前回までに習った線形微分方程式を使って受動素子(抵抗:R、キャパシタ:C、インダクタ:L)のみで構成されたある電気回路の電圧の時間変化を解析する。今回は電圧源に抵抗\(R\)とインダクタ\(L\)が直列につながれた場合のRL回路について考える。
インダクタンスのインピーダンスは\( R_L = L dI(t)/dt \)で表されることから、以下の回路図における微分方程式は
$$ L\frac{dI(t)}{dt} + RI(t) = E(t) (1) $$となる。ソースとなる\( E(t)\)は外力項であることに注意。(つまり、ソースがない状態での回路の特性は左辺の微分方程式によって記述され、のちに学ぶラプラス変換により微分方程式の簡略化と周波数特性を表す伝達関数を求めることができる。)
回路が外部の電流源、あるいは電圧源につながれている状態の微分方程式は非同次系となり今回のRL回路に関して解くべき微分方程式は(非同次系)一階線形常微分方程式\( y’ + q(x)y = f(x)\)である。
前回学んだ通り、非同次系の線形微分方程式は同次系の一般解と非同次系の特殊解の和 \( y(x) = z(x) + u(x) \)によって表すことができる。同次系の一般解はもっとも簡単で、公式\( z(x) = C\int q(x) dx \)より得る。非同次系の特殊解は定数変化法と未定係数法があるが、係数が定数かつ外力項が決まった形であれば積分計算を伴う定数変化法よりも、恒等式から導ける連立方程式で解く未定係数法の方が簡単なのであった。よって、今回は電流源が直流(時間変化しない)\( E(t) = E_0 \)と交流 \(E(t) = E_0 \cos{\omega t}\)にわけて本題を解いていく。なお、同次系一般解\( z(x)\)は共通であり、公式を用いて
$$ z(t) = C\exp{-\tau t} $$となる。ただし、\( \tau = \frac{L}{R} \)とおいた。これを時定数と呼ぶ。
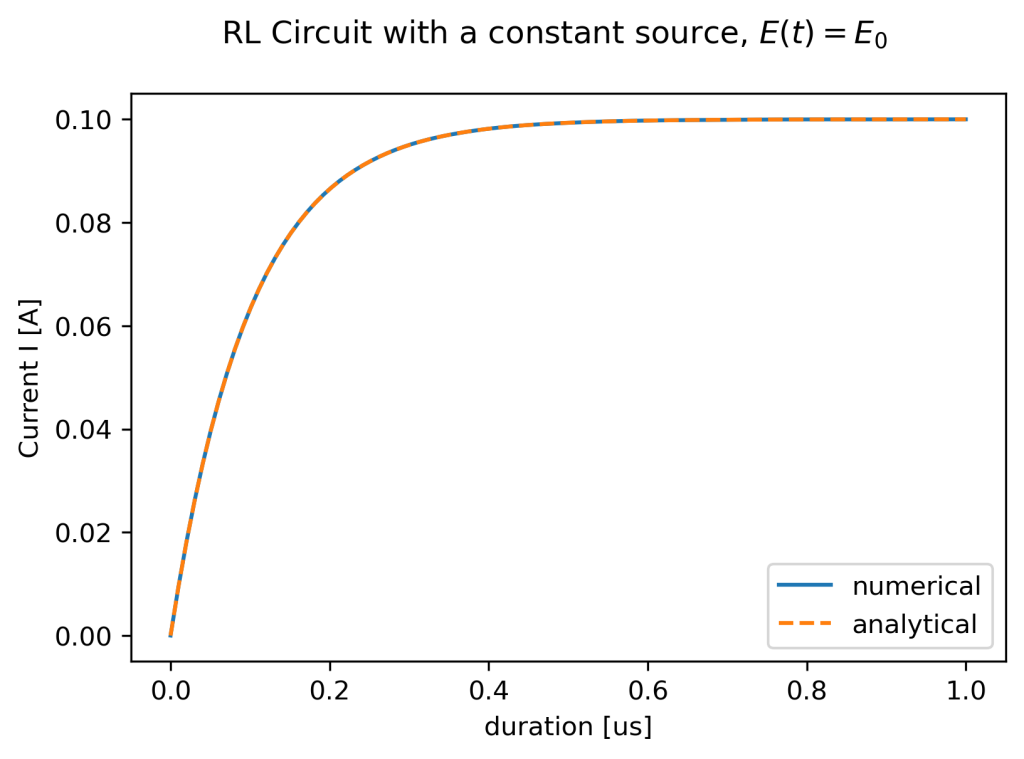
直流電流源の場合の非同次系特殊解
$$ L\frac{dI(t)}{dt} + RI(t) = E_0, (I.C.: I(t) = 0) $$外力項が定数\(E(t) = E_0 \)の場合、未定係数法により、\( u(t) = C_0\)と置き、これをもとの微分方程式(1)に代入することで、\(u(t) = C_0 = E_0/R \)が得られる。すでに求まっている\( z(t) \)と組み合わせることで
$$ I(t) = C\exp{(-R/Lt)} + \frac{E_0}{R} $$これで、微分方程式の一般解が求まった。あとは初期条件により、この回路の電流時間特性を求めることができる。たとえば、初期条件(Initical Condition)が\( I(t) = 0\)のように与えられているとしたら、これを上の式に代入すれば、\( C = -E_0/R\)となり、最終的に
$$ I(t) = \frac{E_0}{R}(1 – \exp{(-R/Lt)} $$であることが分かる。この結果の物理的な解釈としては、インダクタを構成するコイルは流れる電流が時間変化するときのみ、逆起電力が生じるので、ソースの電流元が直流であることからも、接続した瞬間の立ち上がりをのぞけば電流の時間変化は起こらず、逆起電力も生じないので回路に影響を与えなくなるということが説明できる。実際、\( t -> \inf \)において、特殊解の第二項は0となり、以降、回路を流れる電流の大きさは起電力と抵抗からオームの法則により求まる\( I(t) = E_0/R \)となる。直流源では十分な時間がたった後、コンデンサはショート(短絡)となることを数学的に示している好例である。(ちなみに、のちにRC回路で示すことだが、キャパシタは十分な時間が経つとオープン(開放)となる。)
交流電流源の場合の非同次系特殊解
次に、ソースとなる電流源が交流で回路に周波数\(f [Hz]\)の電流が流れると仮定する。このとき、外力項である\(E(t)\)は\(E(t) = E_0\sin{\omega t}\)とあらわされ、RL回路の微分方程式は以下のようになる。
$$ L\frac{dI(t)}{dt} + RI(t) = E_0\sin{\omega t}, (I.C.: I(t) = 0) (2) $$外力項が三角関数のとき、未定係数法で$$u(t) = A\sin{\omega t} + B\cos{\omega t}$$とおけば、(1)式に代入することにより非同次系の特殊解が恒等式により得られる。
$$ \begin{eqnarray} -B\omega + \frac{R}{L}A &=& \frac{E_0}{L} \\ A\omega + \frac{R}{L}B &=& 0 \end{eqnarray} $$これらを整理すると、
$$ \begin{eqnarray} A &=& \frac{E_0 R}{R^2 + (\omega L)^2} \\ B &=& \frac{-\omega L E_0}{R^2 + (\omega L)^2} \end{eqnarray} $$となり、非同次系の特殊解\( u(t) = \frac{E_0}{R^2 + (\omega L)^2}(R\sin{\omega t} + \omega L\cos{\omega t} \)と求まる。このままでは見づらいので、三角関数の合成公式を用いると、
$$ u(t) = \frac{E_0}{\sqrt{R^2 + (\omega L)^2}}\sin{(\omega t – \delta)},\hspace{10pt} \delta = \tan^{-1}{\frac{\omega L}{R}} $$と三角逆関数を使って位相のズレ\( \delta \)を表すと上記のようにきれいにまとまる。
\(R = 10 [\mathrm{Ohm}], L = 1[\mu \mathrm{H}], \mathrm{f} = 1 [\mathrm{MHz}] \)
のときの解析解と数値解を以下に示す。
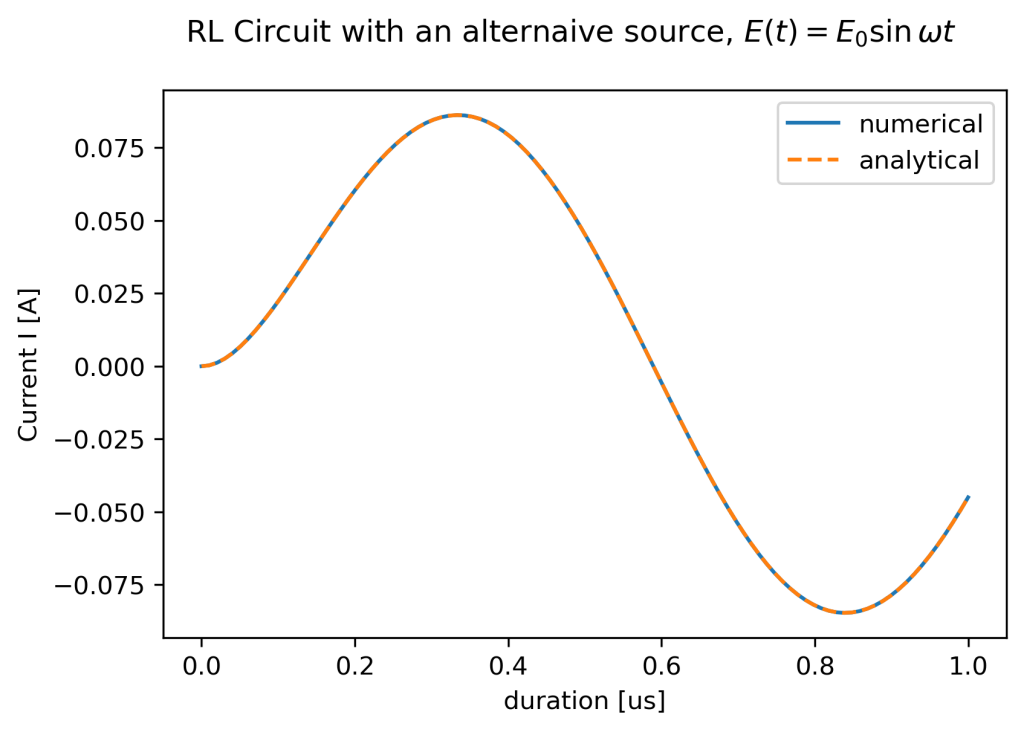
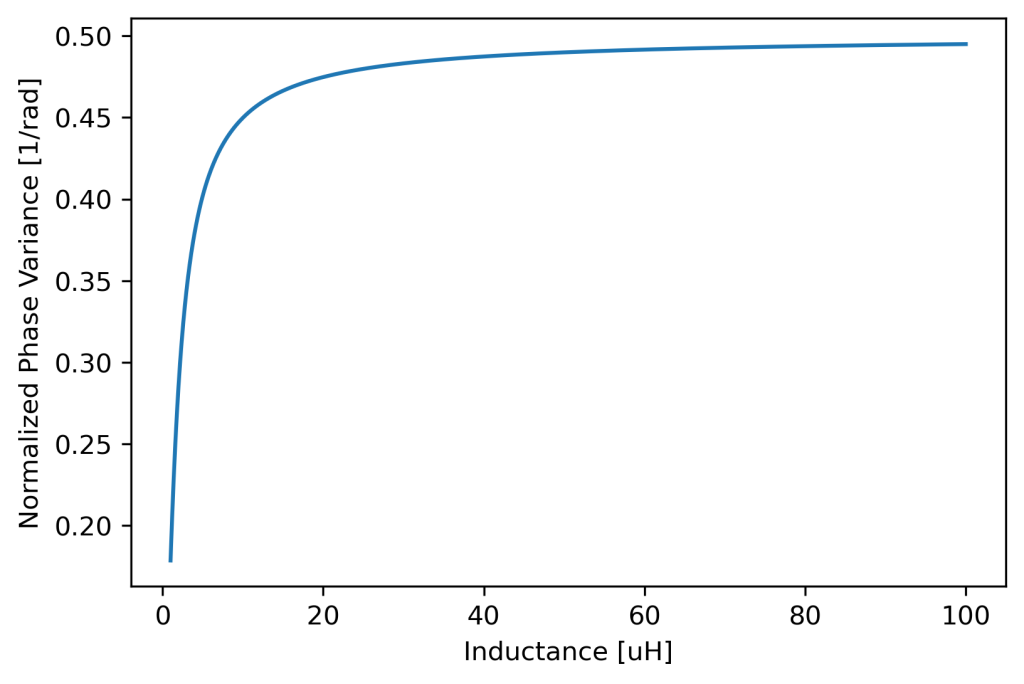
合成三角関数による\(\delta = \tan^{-1}{\frac{\omega L}{R}}\)により見通しがよくなったおかげで、インダクタを挿入することにより、回路を流れる交流信号の位相がどの程度ずれるか定量的に計算することができる。ちなみに、上記の例では計算により位相が32度進んでいることがわかる。インダクタンスを大きくする、あるいは周波数をあげることで位相のずれは大きくなり、最終的に\( \frac{\pi}{2}\)だけ位相が進む。周波数1 MHzのときのインダクタンスの大きさと位相のずれの関係を以下のグラフに示す。
今回、RL回路解析用に書いたPythonコードを以下に載せる
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
exp,sin,cos,arctan,sqrt = [np.exp,np.sin,np.cos,np.arctan,np.sqrt]
"""
RL Circuit
Constant current source
"""
E0 = 1
V = lambda t:E0
def function(t,y,V,R,L): return (V(t)-R*y)/L
t0,t1 = [0,1e-6]
R,L = [10,1e-6]
t = np.linspace(t0,t1,100)
sol_function = solve_ivp(lambda t,y:function(t,y,V,R,L), [t0,t1], [0],t_eval = t)
def y(t,R,L):
tau = L/R
return E0/R*(1-exp(-t/tau))
fig,ax = plt.subplots()
ax.plot(t*1e6,sol_function.y[0])
ax.plot(t*1e6,y(t,R,L),'--')
ax.legend(['numerical','analytical'])
fig.suptitle(r"RL Circuit with a constant source, $E(t) = E_0$")
ax.set_xlabel('duration [us]')
ax.set_ylabel('Current I [A]')
"""
RL Circuit
Alternative current source
"""
f = 1e6
V = lambda t,f:sin(2*pi*f*t)
def function4(t,y,V,R,L,f): return (V(t,f)-R*y)/L
t0,t1 = [0,1e-6]
R,L = [10,1e-6]
t = np.linspace(t0,t1,100)
sol_function4 = solve_ivp(lambda t,y:function4(t,y,V,R,L,f), [t0,t1], [0],t_eval = t)
a = R/(2*pi*f*L)
def y4(t,R,L,f):
tau = L/R
#delta = arctan(2*pi*f*L/R)
#c = 1/sqrt(R**2 + (2*pi*f*L)**2)*sin(delta)
omega = 2*pi*f
theta = arctan(omega*L/R)
C = 1/sqrt(R**2 + (omega*L)**2)*sin(theta)
return C*exp(-t/tau) + 1/sqrt(R**2 + (omega*L)**2)*sin(omega*t - theta)
fig,ax = plt.subplots()
ax.plot(t*1e6,sol_function4.y[0])
ax.plot(t*1e6,y4(t,R,L,f),'--')
ax.legend(['numerical','analytical'])
fig.suptitle(r"RL Circuit with an alternaive source, $E(t) = E_0\sin{\omega t}$")
ax.set_xlabel('duration [us]')
ax.set_ylabel('Current I [A]')
"""
Phase variance as inductance varies at the frequency of 1 MHz
"""
L = np.linspace(1e-6,100e-6,1000)
fig,ax = plt.subplots()
ax.plot(L*1e6,arctan(2*pi*f*L/R)/pi)
ax.set_xlabel("Inductance [uH]")
ax.set_ylabel("Normalized Phase Variance [1/rad]")